Absolutely loved listening to the latest podcast while I was coming back from visiting dad. I suddenly had a brain wave. Thinking about the conventional model of reality. Gravity and Centrifugal motions of each and every celestial body as they spin around themselves, other larger bodies and the push and pull of gravities at their respective masses interact. Wow what a complex system! In fact it's much more fun to do a deep dive on how this system is supposed to work. I will present some detail on why this model for our reality does not make sense.

Now I've made a couple of videos, which quite honestly have no bells and whistles but to go through even the basic concepts needs graphics! But let's try and sketch it out here. The next step past the sketch is to do the math. I've heard our astrophysicists cannot create stable mathematical models of all the bodies interacting with their respective masses. But moving on....

Let's take two conventionally understood forces acting on Earth (but not limited to). Gravity and Centrifugal Motion. Now gravity works the same and by the same amount for any given mass located anywhere on the sphere. In this presentation I'd like to focus on the Poles (tips of the rotational axis of the "planet") and the Equator (the center circle marking out the greatest perpendicular distance from the planet's rotational axis. Now as I mentioned gravity works the same no matter where we are on the surface. So if you weigh 70 kg in Indonesia (on the Equator) you weigh 70 kg at the South Pole (since that's where there's land for you to stand on right?).

Initially I asked Google's Bard AI to give me the formula but they were incorrect. So I went to ChatGTP and it gave me the correct formulas.

* The formula for the gravitational force exerted on an object near the surface of the Earth can be calculated using the following equation:

Gravitational force = (mass of the object) x (acceleration due to gravity) (Newtpms or kg .m/s^2)

On the surface of the Earth, the standard value for the acceleration due to gravity is approximately 9.8 meters per second squared (m/s^2).

For an adult human male, the mass can vary, but let's assume an average mass of around 70 kilograms (kg).

Using these values, the gravitational force exerted on an adult human male standing on the surface of the Earth can be calculated as:

Gravitational force = (70 kg) x (9.8 m/s^2)

Gravitational force ≈ 686 Newtons (N)

Therefore, the approximate gravitational force exerted on an adult human male standing on the surface of the Earth is 686 Newtons.

* Next step. Let's look at Centrifugal force. According to Bard (Google's AI) "Centrifugal force is an apparent force that acts outward on a body moving in a circular path. It is directed away from the center of the circle. ".

But Bard's formula was wrong so copied below is the formula given by ChatGTP.

The formula for centrifugal force can be calculated using the following formula:

Centrifugal force = (mass) x (rotational speed)^2 x (radius) (Newtons or kg.m(radians per second)^2 Correct!

In this formula:

• "mass" refers to the mass of the object or particle experiencing the centrifugal force. (kg)

• "rotational speed" represents the angular velocity of the object or particle, measured in radians per unit of time (e.g., seconds).

• "radius" denotes the distance between the object's axis of rotation and the object itself. (m)

The units of Centrifugal force will be Newtons.

Even though both Bard and ChatGTP said these are not real forces we will continue as we know from our childhood memories that falling a Merry-Go-Round that Centrifugal Force is real enough that it hurts!

NOTE: The radius in the first equation is not the same as the radius in the second.

For gravity the radius is fixed as the radius of the "sphere" of Earth.

For centrifugal motion the radius depends on the angle of the position on the surface relative to the axis of rotation.

What does this mean?

At the North pole (not magnetic) but on the tip of the axis. The angle is zero relative to the rotational axis. So the ``radius" is zero meters. Notice if you drop that into the formula you get zero Centrifugal force. We know this is true from life experience. But at an angle of 90 degrees relative to the rotational axis you are placed right on the equator. So the result from the same formula gives you the maximum Centrifugal Force. Again we understand this intuitively.

So what am I saying? I’m saying what everyone , who thinks about it with an open mind, already understands. Although our so-called Gravity is constant and on its own might explain why we have the same weight wherever we are on the “globe”. If you add the effect of centrifugal motion everything varies. Your perceived weight will be lightest on the equator where the centrifugal force is at a maximum. But as we move across the surface towards either pole end we would gradually feel heavier as the effects of centrifugal force decrease. But not only that, the centrifugal force would no longer be perpendicular to the earth’s surface but gradually tilt at an angle to zero degrees or horizontal as it decreases in magnitude.

What a strange sensation that would be?

I will hand draw a set of images to attempt to show you what I mean.

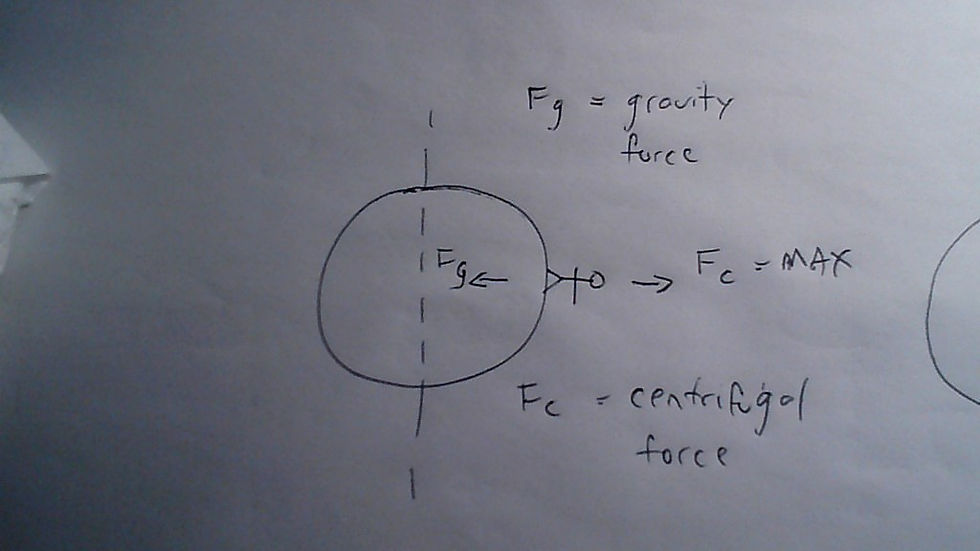
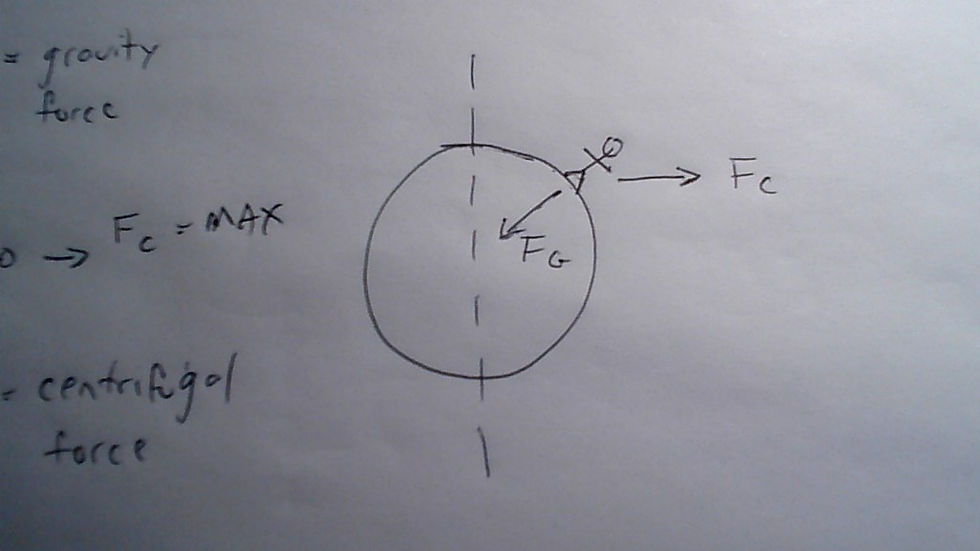
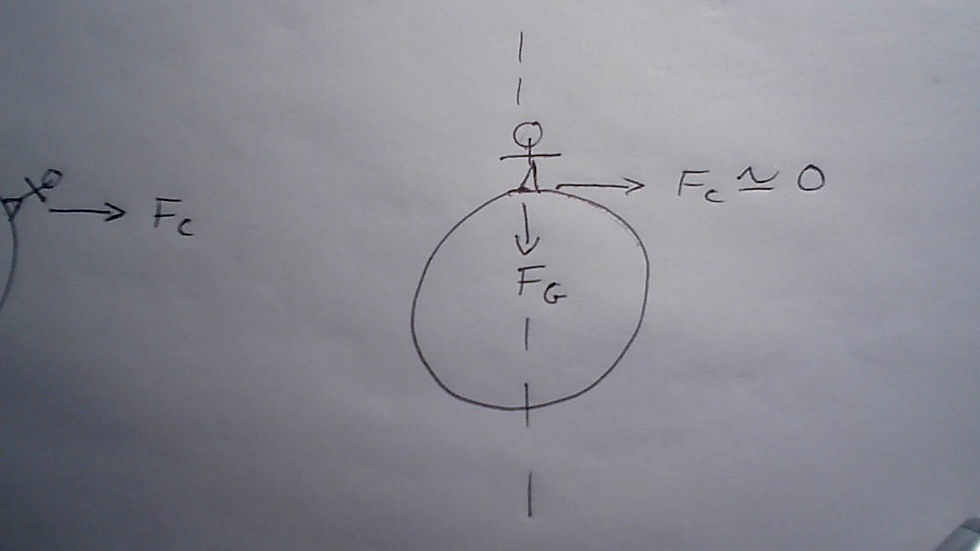
Clearly depending on where a person is standing the combined total force and it’s direction changes. Since I have provided the formulas it is possible to do some initial calculations. With trigonometry to calculate the exact values and directions. Since it’s late I will stop for now. But I think this expands on our intuitive understanding that the spinning globe model just doesn’t work.